|
Evo Design - structural design
|
Calculation No.
|
|
|
| |
|
|
|
|
|
|
|
|
001-BASEPLATE
|
|
|
CALCULATION SHEET
|
Project No.
|
|
|
|
| |
|
|
|
|
|
onlinestructuraldesign.com
|
SAMPLE CALCULATION
|
|
|
Project Title:
|
Base plate calculation interactive online spreadsheet
|
|
Calc. By
|
Date
|
Rev.
|
|
| |
|
|
|
|
|
|
|
|
MN
|
16.04.2014
|
0
|
|
|
Subject/Feature:
|
Column Base Plate Design - Online Calculation Report
|
|
Checked By
|
Date
|
|
|
| |
|
|
|
|
|
|
|
|
CN
|
16.04.2014
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
per EN 1992-1-1, EN 1993-1-1 and EN 1993-1-8
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Input
|
Output
|
|
|
|
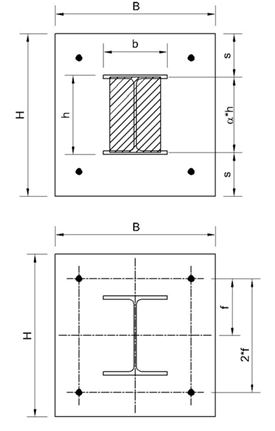
Base plate size in plan
|
Base plate thickness
|
|
|
|
Column base forces
|
Max. pressure under baseplate
|
|
|
|
Materials (steel, concrete, bolts)
|
Max. tension in bolts / bolt verification
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Profile dimensions
|
|
|
|
|
|
|
|
|
|
|
|
|
h =
|
|
mm
|
profile height
|
|
|
|
|
|
|
|
|
|
b =
|
|
mm
|
profile width
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Base Plate Dimensions
|
|
|
|
|
|
|
|
|
|
|
|
|
H =
|
|
mm
|
|
|
|
|
|
|
|
|
|
|
|
B =
|
|
mm
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Base plate thickness is determined in the calculation
|
|
|
|
|
|
|
|
|
|
s =
|
|
mm
|
critical section location
|
|
|
|
|
|
|
|
| |
|
|
(usually in the middle of the flange)
|
|
|
|
|
|
|
|
Bolt locations on plate
|
|
|
|
|
|
|
|
|
|
|
|
|
f =
|
|
mm
|
|
|
|
|
|
|
|
|
|
|
|
nB
=
|
2
|
|
number of hold down bolts (bolts in tension)
|
|
|
|
|
|
|
|
f =
|
20
|
mm
|
bolt diameter
|
|
|
|
|
|
|
| |
(parameters that can not be modified in the demo version)
|
|
|
|
|
|
|
|
Materials
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Steel bolt characteristics
|
|
|
|
|
|
|
per EN 1993-1-8
|
|
|
Bolt class
|
|
|
|
|
|
|
|
Section 3 Table 3.1
|
|
| |
|
|
|
|
|
|
|
bolt classes recommended by the Eurocode;
|
|
|
Bold yield strength
|
|
|
|
|
|
|
The National Annex may exclude certain bolt classes.
|
|
|
fyb
=
|
|
N/mm2
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
Partial factor for steel bolts
|
|
|
|
|
|
per EN 1993-1-8
|
|
|
gM2 =
|
|
|
|
|
|
|
|
Section 2 Table 2.1
|
|
| |
|
|
|
|
|
|
|
partial safety factors recommended by the Eurocode;
|
|
|
Bolt design strength
|
fyd = fy / gM2
|
|
|
|
|
Numerical values for safety factors may be defined
|
|
|
fyd-b
=
|
|
N/mm2
|
|
|
|
|
|
in the National Annex
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Steel base plate characteristics
|
|
|
|
|
|
|
|
|
|
|
|
Steel grade
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Steel yield strength
|
|
|
|
|
|
|
|
|
|
|
|
|
fy
=
|
|
N/mm2
|
for thickness under 40mm
|
|
|
|
|
|
|
|
fy
=
|
|
N/mm2
|
for thickness between 40mm and 80mm
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Partial factor for steel elements (in bending)
|
|
|
|
|
per EN 1993-1-1
|
|
|
gM0 =
|
|
|
|
|
|
|
|
Section 6.1 (1) and Note 2B
|
|
| |
|
|
|
|
|
|
|
value recommended by the Eurocode; value to be
|
|
| |
|
|
|
|
|
|
|
used can be found in the Eurocode National Annex
|
|
|
References:
|
|
|
Design of Welded Structures - O. W. Blodgett (James F. Lincoln Arc Welding Foundation)
|
|
|
EN 1992-1-1:2004 - Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings
|
|
|
EN 1993-1-1:2005 - Eurocode 3: Design of steel structures - Part 1-1: General rules and rules for buildings
|
|
|
EN 1993-1-8:2005 - Eurocode 3: Design of steel structures - Part 1-8: Design of joints
|
|
|
|
|
|
|
|
|
Calculation No.
|
|
|
|
|
|
|
CALCULATION SHEET
|
Project No.
|
|
|
|
| |
|
|
|
|
|
onlinestructuraldesign.com
|
|
|
|
Project Title:
|
|
|
Calc. By
|
Date
|
Rev.
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Subject
|
|
|
Ckd. By
|
Date
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Steel modulus of elasticity
|
|
|
|
per EN 1993-1-1
|
|
|
Es
=
|
210000
|
N/mm2
|
|
|
|
|
|
Section 3.2.6 (1)
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Concrete characteristics
|
|
|
|
|
|
|
|
|
|
Concrete class
|
|
|
|
|
|
|
per EN 1992-1-1:2004
|
|
|
fck
=
|
|
MPa
|
concrete characteristic cylinder strength
|
|
Section 3 Table 3.1
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Partial factor for concrete for ultimate limit states
|
|
|
|
per EN 1992-1-1:2004
|
|
| |
|
|
|
|
|
|
|
Section 2 Table 2.1N
|
|
|
gc =
|
|
|
|
|
|
|
|
values for Persistent & Transient design situations
|
|
| |
|
|
|
|
|
|
|
recommended by the Eurocode; values to be used
|
|
| |
|
|
|
|
|
|
|
may be found in the Eurocode National Annexes
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Design compressive concrete strength
|
|
|
|
per EN 1992-1-1:2004
|
|
| |
|
|
|
|
|
|
|
Section 3.1.6 & Formula 3.15
|
|
|
acc =
|
|
|
|
|
|
|
|
Coefficient taking account of long term effects
|
|
|
fcd
=
|
acc * fck / gc
|
=
|
|
MPa
|
|
|
on the compressive strength and of unfavourable
|
|
| |
|
|
|
|
|
|
|
effects resulting from the way the load is applied
|
|
| |
|
|
|
|
|
|
|
value may be found in the EC National Annex
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Concrete modulus of elasticity
|
|
|
|
|
|
|
|
|
|
Ecm
=
|
|
GPa for
|
concrete class
|
|
|
|
per EN 1992-1-1:2004
|
|
| |
|
|
|
|
|
|
|
Section 3.1.3 Table 3.1
|
|
|
Aggregates =
|
|
|
|
|
|
|
Section 3.1.3 (2)
|
|
| |
|
|
|
|
|
|
|
Values in Table 3.1 are given for quartzite aggregates
|
|
|
Ecm
=
|
|
|
|
Values for limestone and sandstone are reduced
|
|
|
Ecm
=
|
|
N/mm2
|
|
|
|
|
|
by 10% and 30% respectively. For basalt aggregates
|
|
| |
|
|
|
|
|
|
|
the value should be increased by 20%
|
|
|
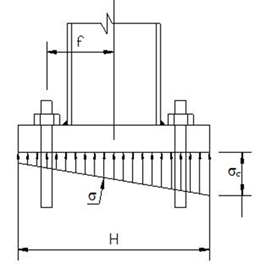
Column base forces
|
|
|
|
|
|
|
|
|
|
|
|
N =
|
|
kN
|
axial force
|
|
|
|
pair of column base forces. Mx and My are not
|
|
|
M =
|
|
kN*m
|
bending moment
|
|
|
|
considered simultaneous.
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
e =
|
M/F =
|
|
mm
|
|
|
|
|
|
|
|
|
|
H/6 =
|
|
mm
|
eccentricity
|
|
|
|
|
|
|
|
|
|
e
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
References:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Design of Welded Structures - O. W. Blodgett (James F. Lincoln Arc Welding Foundation)
|
|
|
EN 1992-1-1:2004 - Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings
|
|
|
EN 1993-1-1:2005 - Eurocode 3: Design of steel structures - Part 1-1: General rules and rules for buildings
|
|
|
EN 1993-1-8:2005 - Eurocode 3: Design of steel structures - Part 1-8: Design of joints
|
|
|
|
|
|
|
|
|
Calculation No.
|
|
|
|
|
|
|
CALCULATION SHEET
|
Project No.
|
|
|
|
| |
|
|
|
|
|
onlinestructuraldesign.com
|
|
|
|
Project Title:
|
|
|
Calc. By
|
Date
|
Rev.
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Subject
|
|
|
Ckd. By
|
Date
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
sc =
|
N/HB+6*M/B*H2
|
|
|
|
|
|
|
|
|
|
|
|
sc =
|
|
MPa
|
|
|
|
|
|
|
|
|
|
|
|
sc
|
|
fcd
|
|
fcd
=
|
|
MPa
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Design of the Base Plate Thickness
|
|
|
|
|
|
|
|
|
|
|
|
Critical section location
|
|
|
|
|
|
|
|
|
|
|
|
s =
|
|
mm
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
smin =
|
|
MPa
|
|
|
|
|
|
|
|
|
|
|
|
ssc =
|
smin+(sc-smin)*(H - s) / H =
|
|
MPa
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Design critical moment - at critical section
|
|
|
|
|
|
|
|
|
|
|
MEd.plate =
|
[(σsc*s/2)*(s/3)+(σc*s/2)*(s*2/3)]*B =
|
|
kN*m
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Calculation No.
|
|
|
|
|
|
|
CALCULATION SHEET
|
Project No.
|
|
|
|
| |
|
|
|
|
|
onlinestructuraldesign.com
|
|
|
|
Project Title:
|
|
|
Calc. By
|
Date
|
Rev.
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Subject
|
|
|
Ckd. By
|
Date
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
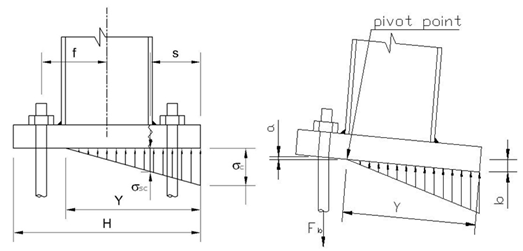
Three equations, three unknowns:
|
Fb,
Y, sc
|
|
|
|
|
|
|
|
|
|
|
(Axial force in steel hold down bolts, active area
|
|
|
|
|
|
|
|
|
|
|
under base plate, aximum pressure under base plate)
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Forces equilibrium
|
|
|
|
|
|
|
|
|
|
| |
Y*sc/2 - Fb -N = 0
|
|
|
|
|
|
|
|
|
|
|
| |
Fb + N = Y*sc*B/2
|
(1)
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Bending moment equilibrium
|
|
|
|
|
|
|
|
|
|
| |
Fb * f + (Fb + N) * (H/2 - Y/3) - N * e = 0
|
|
|
|
|
|
|
|
| |
Fb = -N * (H/2 - Y/3 -e)/(H/2 - Y/3 + f)
|
|
|
(2a)
|
|
|
|
|
| |
N = -Fb * (H/2 - Y/3 -e)/(H/2 - Y/3 + f)
|
|
|
(2)
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Representing the elastic behaviour of the concrete
|
|
|
|
|
|
|
|
|
support and the steel hold-down bolt:
|
|
|
|
|
|
|
|
| |
a/b =
|
eb/ec =
|
(sb / Es) / (sc / Ec)
|
|
|
|
|
|
|
|
|
| |
since
|
Es =
|
sb / es
|
|
|
|
modulus of elasticity of steel bolt
|
|
| |
|
Ec =
|
sc / ec
|
|
|
|
modulus of elasticity of concrete
|
|
| |
|
nb =
|
|
|
|
|
|
number of steel hold down bolts
|
|
| |
|
Ab =
|
|
p*f2/4 =
|
|
mm2
|
|
area of steel hold down bolts
|
|
| |
|
sb =
|
Fb /
Ab
|
|
|
|
|
|
|
|
|
|
| |
|
n =
|
Es /
Ec =
|
|
|
|
|
modular ratio of elasticity, steel to concrete
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
a/b =
|
(N/Ab)/(sc*n) =
|
N/(Ab*sc*n)
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
From similar triangles
|
|
|
=>
|
|
|
|
|
|
|
| |
a/b =
|
(H/2-Y+f)/Y
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
=>
|
N/(Ab*sc*n) =
|
(H/2-Y+f)/Y
|
=>
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
=>
|
sc =
|
Fb * Y / (Ab * n *(H/2 - Y + f))
|
|
|
(3)
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
From (1), (2) and (3)
|
|
|
|
|
|
|
|
|
|
|
|
| |
-Fb * (H/2 - Y/3 -e)/(H/2 - Y/3 + b) + Fb =
|
(Fb * Y2 * B) / [2 * Ab * n *(H/2 - Y + f)]
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Solve for Y:
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Y3 + 3 * (e - H/2) * Y2 + [(6 * n * Ab)/B] * (f + e) * Y
- [(6 * n * Ab)/B] * (H/2 + f) * (f + e) = 0
|
|
| |
or
|
|
|
|
|
|
|
|
|
|
|
|
| |
Y3 + K1 * Y2 + K2 * Y + K3 = 0
|
|
| |
where
|
|
|
|
|
|
|
|
|
|
|
|
| |
K1 =
|
3 * (e - H/2) =
|
|
|
|
|
|
|
|
|
| |
K2 =
|
[(6 * n * Ab)/B] * (f + e) =
|
|
|
|
|
|
|
|
|
| |
K3 =
|
- K2 * (H/2 + f) =
|
|
|
|
|
|
|
|
|
| |
Y =
|
|
mm
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
References:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Design of Welded Structures - O. W. Blodgett (James F. Lincoln Arc Welding Foundation)
|
|
|
EN 1992-1-1:2004 - Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings
|
|
|
EN 1993-1-1:2005 - Eurocode 3: Design of steel structures - Part 1-1: General rules and rules for buildings
|
|
|
EN 1993-1-8:2005 - Eurocode 3: Design of steel structures - Part 1-8: Design of joints
|
|
|
|
|
|
|
|
|
Calculation No.
|
|
|
|
|
|
|
CALCULATION SHEET
|
Project No.
|
|
|
|
| |
|
|
|
|
|
onlinestructuraldesign.com
|
|
|
|
Project Title:
|
|
|
Calc. By
|
Date
|
Rev.
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Subject
|
|
|
Ckd. By
|
Date
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Fb
=
|
|
kN (in
|
|
|
|
|
per (2a) hold down bolts max. tension (in all bolts)
|
|
|
F1.bolt = Fb /
|
|
|
kN
|
|
|
|
|
hold down bolt max. tension - in 1 bolt
|
|
|
F1.bolt /(p*f2/4) =
|
|
N/mm2
|
|
fyd-b
|
|
|
|
|
| |
|
|
|
|
|
N/mm2
|
|
|
|
|
|
|
|
sc =
|
|
MPa
|
|
|
|
|
|
per (3)
|
|
|
|
|
|
sc
|
|
fcd
|
|
fcd
=
|
|
MPa
|
|
effective max. pressure under baseplate is compared
|
|
|
|
|
with the concrete design compressive strength
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Design of the Base Plate Thickness
|
|
|
|
|
|
|
|
|
|
|
|
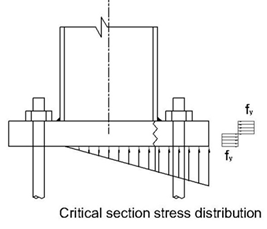
Critical section location
|
|
|
|
|
|
|
|
|
|
|
|
s =
|
|
mm
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Stress at the critical section location
|
|
|
|
|
|
|
|
|
|
|
|
ssc =
|
sc*(Y - s) / Y =
|
|
MPa
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Design critical moment - at critical section
|
|
|
|
|
|
|
|
|
|
|
MEd.plate =
|
[(ssc*s/2)*(s/3)+(sc*s/2)*(s*2/3)]*B =
|
|
kN*m
|
|
|
|
|
MEd.plate =
|
(sc*Y/2)*(s-Y/3)*B =
|
|
kN*m
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
MC,Rd = Mpl,rd =
|
(Wpl * fy)/ gM0
|
Bending plastic design resistance
|
|
(4)
|
|
|
|
|
| |
|
|
|
|
|
|
|
per EN 1993-1-1
|
|
| |
|
|
|
|
|
|
|
Section 6.2.5 (2) Formula 6.13
|
|
| |
|
|
|
|
|
|
|
Design resistance for bending about one
|
|
| |
|
|
|
|
|
|
|
principal axis for class 1 or 2 cross sections
|
|
|
Plastic section modulus of rectangular sections
|
|
|
|
|
|
|
|
|
|
|
Wpl
=
|
B*tpl2/4
|
|
|
|
|
|
|
(5)
|
|
|
|
|
|
(tpl = base plate thickness)
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
from (4) and (5)
|
=> [fy * (B*tpl2)/4]/ gM0 > MEd.plate
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
MEd.plate =
|
|
kN*m
|
|
|
|
|
|
|
|
|
|
|
| |
=> tpl > sqrt[4 * MEd.plate * gM0 / (B * fy)]
|
|
|
|
|
|
|
|
|
| |
=> tpl >
|
|
mm
|
(with fy =
|
|
N/mm2)
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
References:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Design of Welded Structures - O. W. Blodgett (James F. Lincoln Arc Welding Foundation)
|
|
|
EN 1992-1-1:2004 - Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings
|
|
|
EN 1993-1-1:2005 - Eurocode 3: Design of steel structures - Part 1-1: General rules and rules for buildings
|
|
|
EN 1993-1-8:2005 - Eurocode 3: Design of steel structures - Part 1-8: Design of joints
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
