|
Evo Design - structural engineering
|
Calculation
No.
|
|
|
|
|
|
001-WOOD COLUMN
|
|
|
CALCULATION SHEET
|
Project No.
|
|
|
|
| |
|
|
|
|
|
onlinestructuraldesign.com
|
SAMPLE
CALCULATION
|
|
|
Project
Title:
|
Wood element - interactive design spreadsheet
|
|
Calc. By
|
Date
|
Rev.
|
|
| |
|
|
|
|
|
|
|
|
MN
|
16.04.2014
|
0
|
|
|
Subject
|
Wood Column Subjected to Combined Compression and
Bending
|
Checked By
|
Date
|
|
|
| |
|
|
|
|
|
|
|
|
CN
|
16.04.2014
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Input
|
Output
|
|
|
|
|
|
|
|
|
|
Element section and dimensions
|
Element verification
|
|
|
|
|
|
|
|
|
|
Material
|
Element stability
|
|
|
|
|
|
|
|
|
|
Loads
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
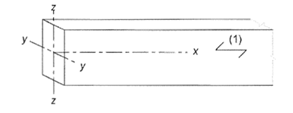
Wood Column
Subjected to Combined Compression and Bending
|
|
per EN
1992-1-1:2004* & EN 338
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Maximum working
loads (Ultimate Limit State)
|
|
|
|
|
|
|
|
|
|
|
FEd=
|
|
kN*m
|
axial force (compression)
|
|
|
|
|
|
|
|
|
|
|
My,Ed=
|
|
kN*m
|
bending moment y-y
|
|
|
|
|
|
|
|
|
|
|
Mz,Ed=
|
|
kN*m
|
bending moment z-z
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
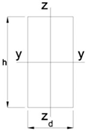
Element dimensions
- Rectangular cross section
|
|
|
|
|
|
|
|
|
|
|
Ly.b =
|
300
|
cm
|
element buckling length about y-y
|
|
|
|
|
|
|
|
|
|
Lz.b =
|
300
|
cm
|
element buckling length about z-z
|
|
|
|
|
|
|
|
|
|
h =
|
20
|
cm
|
height
|
|
|
|
|
|
|
|
|
|
|
|
|
d =
|
10
|
cm
|
width
|
(parameters that can not be modified in the demo
version)
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Section Properties
|
|
|
|
|
|
|
|
|
|
|
A =
|
d*h =
|
|
cm2
|
section area
|
|
|
|
|
|
|
|
IY =
|
d*h3/12 =
|
|
cm4
|
moment of inertia about y-y axis
|
|
|
|
|
|
|
|
Iz =
|
d3*h/12 =
|
|
cm4
|
moment of inertia about z-z axis
|
|
|
|
|
|
|
|
iy =
|
(Iy/A)0.5 =
|
|
cm
|
radius of gyration about y-y
|
|
|
|
|
|
|
|
iz =
|
(Iz/A)0.5 =
|
|
cm
|
radius of gyration about z-z
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ly =
|
Ly.b / iy =
|
|
|
slenderness
ratio corresponding to bending about the y-axis
|
|
|
|
|
lz =
|
Lz.b / iz =
|
|
|
slenderness
ratio corresponding to bending about the z-axis
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Material
characteristics
|
|
|
per EN 338-97 - Table 1
|
|
|
|
|
Wood strength
class:
|
|
|
|
|
|
|
|
|
|
|
|
|
fm,k =
|
|
N/mm2
|
|
|
|
|
|
Characteristic
bending strength
|
|
|
fc,0,k =
|
|
kN/mm2
|
|
|
|
|
|
Characteristic
compressive strength
|
|
|
|
|
E0,05 =
|
|
kN/mm2
|
|
|
|
|
|
Fifth
percentile value of modulus of elasticity
|
|
|
gm =
|
|
|
|
|
|
|
|
per EN 1995-1-1 - Table 2.3
|
|
| |
|
|
|
|
|
|
|
1.3 for
solid timber, 1.25 for glued laminated timber
|
|
|
kh =
|
min( (150/h)0.2 ; 1.3) =
|
|
|
|
|
per EN
1995-1-1 - Section 3.2 (3), formula (3.1)
|
|
| |
|
|
|
|
|
|
for timber
with density less than 700 kg/m3 and
|
|
| |
|
|
|
|
|
|
|
h < 150mm
the characteristic valus of fm,k and
|
|
| |
|
|
|
|
|
|
|
ft,0,k may be increased
by the factor kh
|
|
|
kmod =
|
|
|
|
|
|
|
|
per EN 1995-1-1 - Table 3.1
|
|
| |
|
|
|
|
|
|
|
Load
duration classes per EN 1995-1-1
|
|
| |
|
|
|
|
|
|
|
Section 2.3.1.2 - Table 2.1 and 2.2
|
|
| |
|
|
|
|
|
|
|
Service classes per EN 1995-1-1 - Section 2.3.1.3
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fc.0.d =
|
kmod * fc,0,k
|
/ gm =
|
|
|
N/mm2
|
|
design
compressive strength and
|
|
|
|
|
fm.y.d =
|
fm.y.d =
|
kmod *kh * fm,k
|
/ gm =
|
|
N/mm2
|
|
design
bending strength about y and z axis
|
|
|
|
| |
|
|
|
|
|
|
|
per EN
1995-1-1 - Section 2.4.1, formula (2.14)
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
References:
|
|
|
|
|
EN
1995-1-1:2004 - Eurocode 5: Design of timber structures - Part 1-1: Common
rules and rules for buildings
|
|
|
|
|
|
|
EN
338 : 2003 - Structural Timber; Strength Classes
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Calculation No.
|
|
|
|
|
|
|
|
|
|
|
CALCULATION SHEET
|
Project No.
|
|
|
|
|
|
| |
|
|
|
|
|
onlinestructuraldesign.com
|
|
|
|
|
|
Project Title:
|
|
|
Calc. By
|
Date
|
Rev.
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Subject
|
|
|
Ckd. By
|
Date
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sc,0,d =
|
F,Ed / A =
|
|
N/mm2
|
|
|
|
Design
compressive stress
|
|
|
|
|
sm.y.d =
|
My,Ed * (h/2) / Iy =
|
|
N/mm2
|
|
|
|
Design
bending stress about the principal y axis
|
|
|
|
|
sm.z.d =
|
Mz,Ed * (d/2) / Iz =
|
|
N/mm2
|
|
|
|
Design
bending stress about the principal z axis
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
km =
|
0.7
|
for rectangular sections
|
|
|
|
per EN
1995-1-1 - Section 6.1.6 (2)
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Stresses
verification - Combined bending and axial compression
|
|
per EN
1995-1-1 - Section 6.2.4
|
|
|
|
|
Check on for y-y
axis
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(sc,0,d / fc,0,d )2 + ( sm.y.d / fm.y.d ) + km * ( sm.z.d / fm.z.d ) =
|
|
|
per EN 1995-1-1 - Section 6.2.4, formula (6.19)
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Check on for z-z
axis
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(sc,0,d / fc,0,d )2 + km * ( sm.y.d / fm.y.d ) + ( sm.z.d / fm.z.d ) =
|
|
|
per EN
1995-1-1 - Section 6.2.4, formula (6.20)
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Strability
verification - Combined bending and axial compression
|
|
per EN
1995-1-1 - Section 6.3.2
|
|
|
|
|
Relative
slenderness ratio corresponding to about y axis (deflection in the z
direction)
|
|
|
|
|
|
|
|
lrel,y =
|
(ly /p) *
(fc,0,k / E0,05)0.5=
|
|
|
|
|
per EN
1995-1-1 - Section 6.3.2, formula (6.21)
|
|
|
|
|
Relative
slenderness ratio corresponding to about z axis (deflection in the y
direction)
|
|
|
|
|
|
|
|
lrel,z =
|
(lz /p) *
(fc,0,k / E0,05)0.5=
|
|
|
|
|
per EN
1995-1-1 - Section 6.3.2, formula (6.22)
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bc =
|
|
(0.2 for solid timber and 0.1 for glued laminated
timber)
|
factor per
EN 1995-1-1 - formula (6.29)
|
|
|
|
|
ky =
|
0.5 * (1 + bc * (lrel,y - 0.3) + l2rel,y ) =
|
|
|
|
factor per
EN 1995-1-1 - formula (6.27)
|
|
|
|
|
kz =
|
0.5 * (1 + bc * (lrel,z - 0.3) + l2rel,z ) =
|
|
|
|
factor per
EN 1995-1-1 - formula (6.28)
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kc,y =
|
1 / [ky + (k2y - l2rel,y)0.5] =
|
|
|
|
|
factor per
EN 1995-1-1 - formula (6.25)
|
|
|
|
|
kc,z =
|
1 / [kz + (k2z - l2rel,z)0.5] =
|
|
|
|
|
factor per
EN 1995-1-1 - formula (6.26)
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Check on for y-y
axis
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sc,0,d / ( kc,y * fc,0,d ) + ( sm.y.d / fm.y.d ) + km * ( sm.z.d / fm.z.d ) =
|
|
|
per EN
1995-1-1 - Section 6.3.2, formula (6.23)
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
Check on for z-z
axis
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sc,0,d / ( kc,z * fc,0,d ) + km * ( sm.y.d / fm.y.d ) + ( sm.z.d / fm.z.d ) =
|
|
|
per EN
1995-1-1 - Section 6.3.2, formula (6.24)
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
References:
|
|
|
EN
1995-1-1:2004 - Eurocode 5: Design of timber structures - Part 1-1: Common
rules and rules for buildings
|
|
|
|
|
EN
338 : 2003 - Structural Timber; Strength Classes
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
